↓Skip to main content
  1. Posts/

OpenJDK JVM Deep Dive: A Complete Guide to Java's PRNG Evolution

·4434 words·21 mins
NeatGuyCoding
Author
NeatGuyCoding
Table of Contents

Mastering Random Number Generation: A Complete Guide
#

When we work with random number generators, we typically think of a Pseudo Random Number Generator (PRNG) as a mysterious black box:

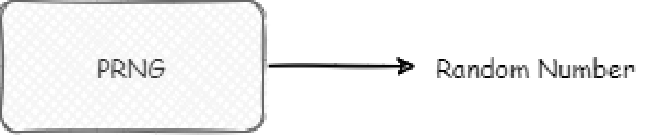
image

This black box outputs numbers, usually integers. The beauty lies in how we can transform these results into any data type we need. Want a long? Simply grab two integers - use one for the high 32 bits and another for the low 32 bits. Need boolean, byte, short, or char values? Just take one integer and extract the relevant bits. For floating-point numbers, we can combine multiple random integers according to IEEE standards to construct both the integer and fractional parts.

When we need to constrain the range, the simplest approach is modulo operation plus offset. For example, to get numbers between 1-100, we take the result modulo 99, get the absolute value, then add 1. Since modulo operations are computationally expensive, there’s a neat optimization: check if N & (N-1) equals 0 - if so, N is a power of 2 (powers of 2 in binary look like 100000…, and subtracting 1 gives 011111…, so the AND operation yields 0). Modulo with powers of 2 can be replaced with bitwise AND operations. This is just one simple optimization - real-world implementations are far more sophisticated.

To initialize our black box, we typically use a SEED value. The source of this seed can vary greatly, but let’s set that aside for now and explore the algorithms inside our black box.

image

Linear Congruential Algorithm
#

Let’s start with the most common random number algorithm: Linear Congruential Generator (LCG). It works by multiplying the current seed by coefficient A, adding offset B, then taking modulo C (to keep results within bounds, allowing us to choose appropriate A and B values - we’ll see why this matters later):

X(n+1) = ( A * X(n) + B ) % C

This algorithm shines with its simplicity and decent performance. The values A and B must be carefully chosen to ensure all numbers within range C appear with equal probability. Consider an extreme example: A = 2, B = 2, C = 10. Here, odd numbers like 1, 3, 5, 7, 9 would never appear in subsequent iterations. To calculate suitable A and B values, we need to constrain C within manageable bounds. For computational efficiency, C is typically set to powers of 2, allowing modulo operations to be optimized into bitwise AND operations. Fortunately, mathematical wizards have already discovered these magic numbers for us - we can simply use their findings!

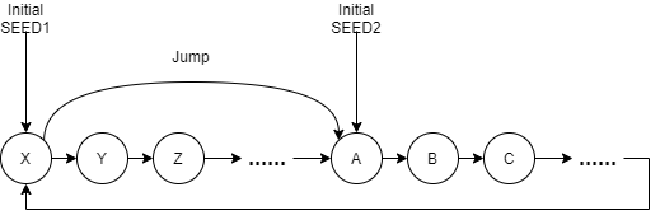
This algorithm generates deterministic random sequences - if X leads to Y, then Y always leads to Z. Think of it as a deterministic loop:

image

The size of this loop is called the Period. With sufficiently large periods and varying initial seeds, we achieve pseudo-randomness. However, when we need multiple random number generators, things get tricky. While we can ensure different initial seeds for each generator, we can’t guarantee that one generator’s seed isn’t just a few steps away from another’s in the sequence. For instance, if one generator starts with seed X and another with Z, even though X and Z might seem vastly different, they could be separated by just one step Y in the algorithm’s sequence. Such generators would perform poorly.

How can we ensure significant separation between different random number generators? We need simple calculations (not computing millions of iterations) to directly create seeds with large gaps. This property is called jumpability. The Xoshiro algorithm, based on Linear Feedback Shift Register algorithms, provides us with jumpable random number generation.

Linear Feedback Shift Register Algorithm
#

A Linear Feedback Shift Register (LFSR) uses the linear function of its previous state’s output as the next input. XOR operations are the most common single-bit linear functions: certain register bits are XORed together as input, then all bits in the register are shifted.

Choosing which bits to use is an art form. Current popular implementations include the XorShift algorithm and its further optimized successor, the Xoshiro family. Xoshiro algorithms are relatively new, optimized random number algorithms with simple calculations, excellent performance, and jumpability.

These algorithms are jumpable. When creating two random number generators with significant separation, we can use a random initial seed for one generator, then use the algorithm’s jump operation to directly generate a well-separated seed for another generator.

image

Another interesting feature: Linear Congruential algorithms aren’t reversible - we can only derive X(n+1) from X(n), not the reverse. This works well for applications like random playlist shuffling, where we only need the current random number to determine the next song. Linear Feedback Shift Register algorithms can be made reversible.

However, LFSR algorithms have limitations when generating different random sequence generators. They still come from the same loop - even with jump operations creating separation, uneven pressure over time might cause different generators to converge to the same seed again. Are there algorithms that can generate completely different random sequence loops?

DotMix Algorithm
#

The DotMix algorithm offers a different approach: given an initial seed, set a fixed step M, and for each random generation, add step M to the seed, then pass it through a hash function to map the value to a hash result:

X(n+1) = HASH(X(n) + M)

This algorithm demands high-quality hash functions that produce dramatically different outputs from slight input changes. The SplitMix algorithm, based on DotMix, uses the MurMurHash3 algorithm - this is the underlying principle of Java 8’s SplittableRandom.

The beauty of this algorithm lies in how we can easily ensure different parameter generators produce different sequences. For example, one might generate 1, 4, 3, 7… while another produces 1, 5, 3, 2. This is something Linear Congruential algorithms can’t achieve - their sequences are deterministic regardless of seed changes, and we can’t freely modify A, B, C values without risking incomplete number coverage. The same applies to Xoshiro. SplitMix algorithms don’t have this concern - different seeds and step sizes M guarantee different sequences. This ability to generate different sequences is called splittability.

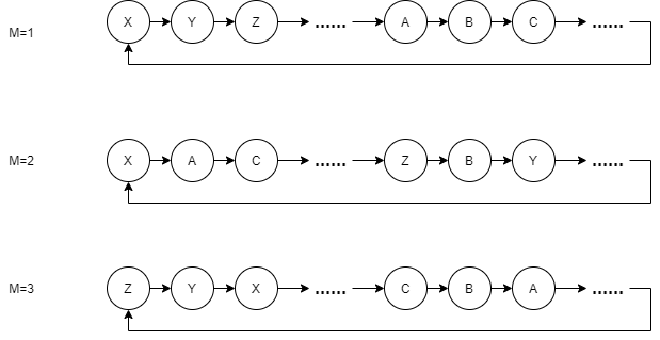
image

This explains why SplittableRandom is better suited for multithreading than Random (which uses Linear Congruential):

  • Multiple threads sharing one Random: ensures sequence randomness but suffers CompareAndSet performance costs for seed updates
  • Each thread using Random with identical seeds: produces identical random sequences per thread
  • Each thread using Random with different seeds: we can’t guarantee one thread’s seed isn’t just the next result (or within a few steps) of another thread’s seed. With uneven thread pressure (thread pools often have only some threads working during quiet periods), certain threads might end up with identical random sequences

Using SplittableRandom, simply call the split interface to assign different parameters to different threads, and different parameters virtually guarantee different sequences.

Thought Exercise: How Do We Generate Sequences with Periods Larger Than Number Capacity?
#

The simplest approach: merge two sequences with periods equal to capacity through round-robin, creating a sequence with Period = capacity + capacity:

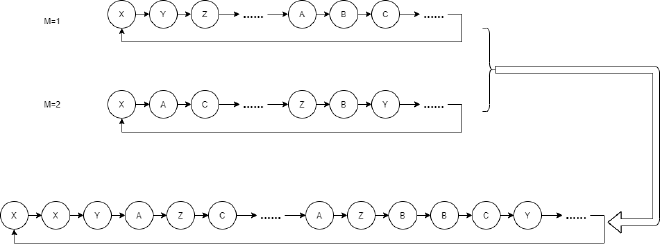
image

We can also record results from two sequences and combine them using operations like XOR or hashing. This gives us Period = capacity * capacity.

For further expansion, we can use these methods to combine different algorithmic sequences, gaining the random advantages of each algorithm. Java 17’s LXM algorithm exemplifies this approach.

LXM Algorithm
#

Introduced in Java 17, the LXM algorithm (L for Linear Congruential, X for Xoshiro, M for MurMurHash) is relatively simple, combining Linear Congruential and Xoshiro algorithms, then hashing with MurMurHash:

  • L34X64M: uses one 32-bit number for Linear Congruential results, two 32-bit numbers for Xoshiro results, then MurMurHash combines these into one 64-bit number
  • L128X256M: uses two 64-bit numbers for Linear Congruential results, four 64-bit numbers for Xoshiro results, then MurMurHash combines these into one 64-bit number

LXM algorithms achieve splittability through MurMurHash but don’t retain Xoshiro’s jumpability.

Seed Sources
#

Since all JDK random algorithms are based on previous inputs, using fixed seeds always produces identical random sequences. This isn’t suitable for security-sensitive scenarios. The official definition of cryptographically secure requires unpredictable seeds producing non-deterministic outputs.

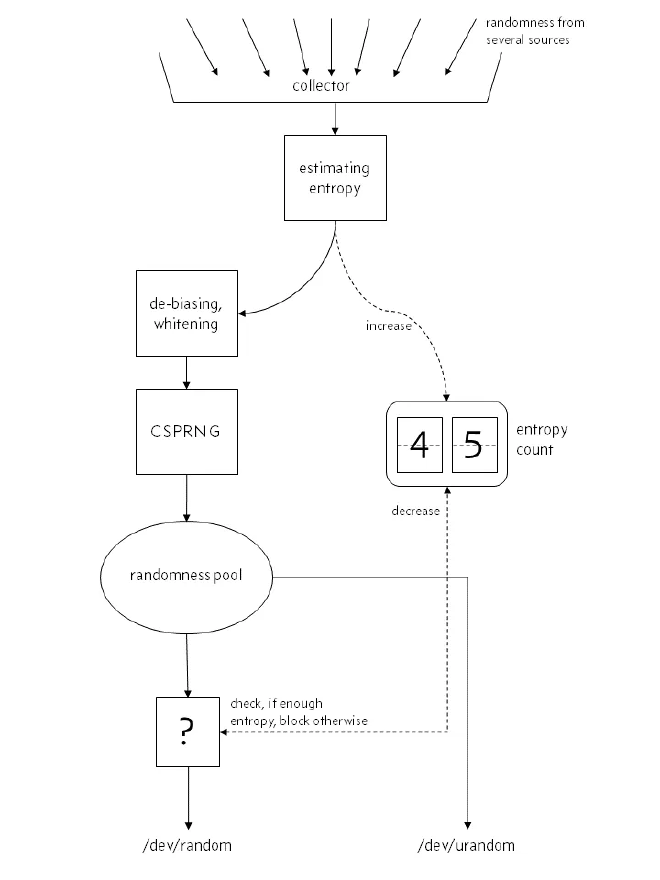
Linux collects user input, system interrupts, and other runtime data to generate random seeds stored in pools that programs can access. However, these pools only generate after collecting sufficient data, have limited size, and don’t guarantee good random distribution. We can’t use them directly for random numbers but as seeds for our random number generators. Linux abstracts these pools as two files: /dev/random and /dev/urandom. One blocks until sufficient entropy is collected, the other returns whatever’s available.

Before Linux 4.8:

image

After Linux 4.8:

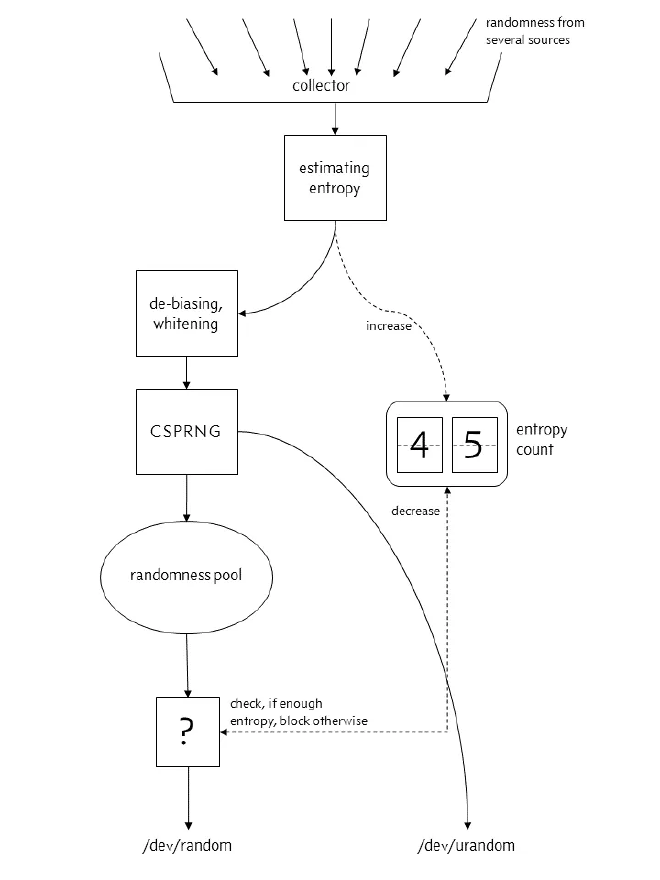
image

When entropy pools are insufficient, /dev/random blocks while /dev/urandom doesn’t. For most purposes, /dev/urandom suffices, so we typically use the JVM parameter -Djava.security.egd=file:/dev/./urandom to reduce blocking.

We can also use business characteristics to periodically reset all Random seeds, further increasing crack resistance. For example, use the past hour’s active users × order count as the new seed every hour.

Testing Random Algorithm Randomness
#

All these algorithms implement pseudo-randomness - current random results strongly correlate with previous ones. Virtually all fast random algorithms work this way.

Even with sufficiently secret seeds, knowing the algorithm still allows predicting next outputs from current ones, or reverse-engineering algorithms from multiple results to predict future outputs.

For pseudo-random algorithms, we need to verify generated random numbers satisfy characteristics like:

  • Maximum possible period: the full cycle or period refers to the number of results needed for the random sequence to traverse all possible outcomes and return to the initial seed. This period should be as long as possible
  • Equidistribution: each possible result should appear the same number of times within one period, ensuring fairness in applications like lotteries
  • Complexity testing: generated sequences should be sufficiently complex, avoiding regular patterns like arithmetic or geometric progressions
  • Security testing: difficulty in reverse-engineering the algorithm from relatively few results

Many frameworks now test and evaluate random sequences from specific algorithms:

Java’s built-in random algorithms basically pass most testU01 tests. Currently, the optimization algorithms mentioned above all expose some randomness issues to varying degrees. Java 17’s LXM algorithm performs best in randomness testing - note this refers to randomness performance, not computational performance.

All Random Algorithms in Java (Excluding SecureRandom)
#

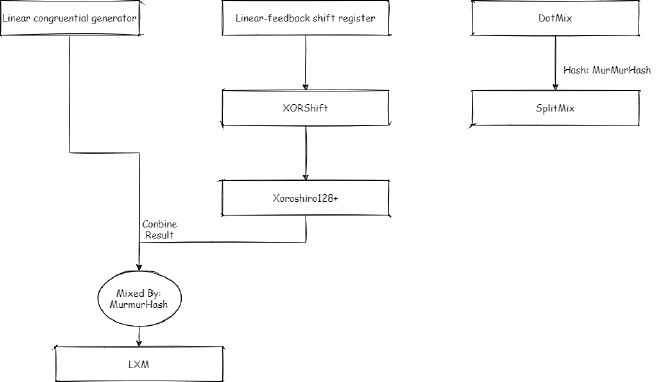
image

Why We Rarely Consider Random Security in Real Business Applications
#

Mainly because we typically deploy multiple instances with load balancing and multithreading. Generally, each thread uses Random instances with different initial seeds (like ThreadLocalRandom). For random-sensitive businesses like lotteries, individual users usually have attempt limits, making it difficult to collect enough results to reverse-engineer algorithms and predict next results - plus you’d be competing with other users. We typically limit random number ranges rather than using raw random numbers, greatly increasing reverse-engineering difficulty. Finally, we can periodically use real-time business metrics to reset seeds, like using (active users × orders) from the past hour as the new seed every hour.

Therefore, in real business scenarios, we rarely use SecureRandom. If we want initial seeds that even programmers can’t guess (timestamps are predictable), we can specify random class initial seed sources through the JVM parameter -Djava.util.secureRandomSeed=true. This affects all Java random number generators (Random, SplittableRandom, ThreadLocalRandom, etc.).

Corresponding source code:

static {
        String sec = VM.getSavedProperty("java.util.secureRandomSeed");
        if (Boolean.parseBoolean(sec)) {
            //Get initial SEED from SecureRandom
            // SecureRandom's SEED source in Linux is /dev/random or /dev/urandom specified by java.security.egd
            byte[] seedBytes = java.security.SecureRandom.getSeed(8);
            long s = (long)seedBytes[0] & 0xffL;
            for (int i = 1; i < 8; ++i)
                s = (s << 8) | ((long)seedBytes[i] & 0xffL);
            seeder.set(s);
        }
    }

So for our business needs, we mainly care about algorithm performance and randomness equidistribution, and since tested algorithms generally have good randomness, we primarily focus on performance.

For security-sensitive businesses like SSL encryption and cryptographic random hash generation, higher security randomness is needed. That’s when we consider SecureRandom, which uses more complex algorithms involving cryptographic concepts - we won’t delve into these secure Random algorithms here.

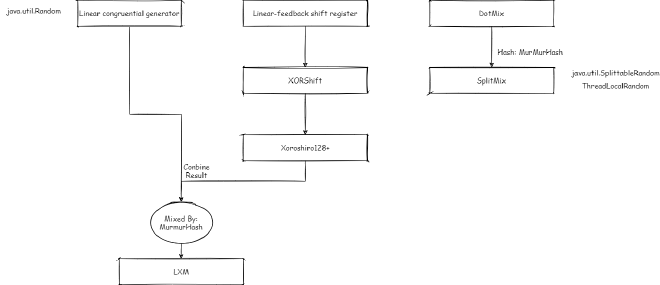
Random Number Generation Before Java 17
#

First, here’s the correspondence between algorithms and implementation classes:

image

Using JDK APIs
#

1. Using java.util.Random and related APIs:

Random random = new Random();
random.nextInt();

Math.random() is also based on Random

java.lang.Math:

public static double random() {
    return RandomNumberGeneratorHolder.randomNumberGenerator.nextDouble();
}
private static final class RandomNumberGeneratorHolder {
    static final Random randomNumberGenerator = new Random();
}

Random is designed to be thread-safe because the seed is atomic and randomization just CAS-updates this seed:

java.util.Random:

protected int next(int bits) {
    long oldseed, nextseed;
    AtomicLong seed = this.seed;
    do {
        oldseed = seed.get();
        nextseed = (oldseed * multiplier + addend) & mask;
    } while (!seed.compareAndSet(oldseed, nextseed));
    return (int)(nextseed >>> (48 - bits));
}

This also shows Random is based on Linear Congruential algorithms

2. Using java.util.SplittableRandom and related APIs

SplittableRandom splittableRandom = new SplittableRandom();
splittableRandom.nextInt();

As analyzed earlier, SplittableRandom implements the SplitMix algorithm - given an initial seed, set a fixed step M, add step M to the seed each time, then hash the value (using MurMurHash3) to map it to a hash result.

SplittableRandom is not thread-safe: java.util.SplittableRandom:

public int nextInt() {
    return mix32(nextSeed());
}   
private long nextSeed() {
    //Not thread-safe here
    return seed += gamma;
}

ThreadLocalRandom is based on SplittableRandom, and we use ThreadLocalRandom in multithreaded environments:

ThreadLocalRandom.current().nextInt();

SplittableRandom can return a completely new SplittableRandom with different parameters and vastly different random sequence characteristics through the split method. We can use these for different threads, which is very common in parallel streams:

IntStream.range(0, 1000)
    .parallel()
    .map(index -> usersService.getUsersByGood(index))
    .map(users -> users.get(splittableRandom.split().nextInt(users.size())))
    .collect(Collectors.toList());

However, due to lack of cache line padding and other multithreading performance optimizations, its multithreaded performance is still worse than ThreadLocalRandom, which is based on SplittableRandom.

3. Using java.security.SecureRandom for higher security randomness

SecureRandom drbg = SecureRandom.getInstance("DRBG");
drbg.nextInt();

These algorithms are typically based on cryptographic algorithms with more complex calculations and poorer performance. They’re only used for highly security-sensitive businesses, not general applications like lotteries.

Performance Testing
#

Single-threaded testing:

Benchmark                                      Mode  Cnt          Score          Error  Units
TestRandom.testDRBGSecureRandomInt            thrpt   50     940907.223 ±    11505.342  ops/s
TestRandom.testDRBGSecureRandomIntWithBound   thrpt   50     992789.814 ±    71312.127  ops/s
TestRandom.testRandomInt                      thrpt   50  106491372.544 ±  8881505.674  ops/s
TestRandom.testRandomIntWithBound             thrpt   50   99009878.690 ±  9411874.862  ops/s
TestRandom.testSplittableRandomInt            thrpt   50  295631145.320 ± 82211818.950  ops/s
TestRandom.testSplittableRandomIntWithBound   thrpt   50  190550282.857 ± 17108994.427  ops/s
TestRandom.testThreadLocalRandomInt           thrpt   50  264264886.637 ± 67311258.237  ops/s
TestRandom.testThreadLocalRandomIntWithBound  thrpt   50  162884175.411 ± 12127863.560  ops/s

Multithreaded testing:

Benchmark                                      Mode  Cnt          Score           Error  Units
TestRandom.testDRBGSecureRandomInt            thrpt   50    2492896.096 ±     19410.632  ops/s
TestRandom.testDRBGSecureRandomIntWithBound   thrpt   50    2478206.361 ±    111106.563  ops/s
TestRandom.testRandomInt                      thrpt   50  345345082.968 ±  21717020.450  ops/s
TestRandom.testRandomIntWithBound             thrpt   50  300777199.608 ±  17577234.117  ops/s
TestRandom.testSplittableRandomInt            thrpt   50  465579146.155 ±  25901118.711  ops/s
TestRandom.testSplittableRandomIntWithBound   thrpt   50  344833166.641 ±  30676425.124  ops/s
TestRandom.testThreadLocalRandomInt           thrpt   50  647483039.493 ± 120906932.951  ops/s
TestRandom.testThreadLocalRandomIntWithBound  thrpt   50  467680021.387 ±  82625535.510  ops/s

Results align with our expectations: ThreadLocalRandom performs best in multithreaded environments. In single-threaded environments, SplittableRandom and ThreadLocalRandom are comparable, both outperforming others. SecureRandom performs hundreds of times worse than others.

Test code follows (Note: although Random and SecureRandom are thread-safe, ThreadLocal is still used to avoid excessive performance degradation from compareAndSet):

package prng;

import java.security.NoSuchAlgorithmException;
import java.security.SecureRandom;
import java.util.Random;
import java.util.SplittableRandom;
import java.util.concurrent.ThreadLocalRandom;

import org.openjdk.jmh.annotations.Benchmark;
import org.openjdk.jmh.annotations.BenchmarkMode;
import org.openjdk.jmh.annotations.Fork;
import org.openjdk.jmh.annotations.Measurement;
import org.openjdk.jmh.annotations.Mode;
import org.openjdk.jmh.annotations.Scope;
import org.openjdk.jmh.annotations.State;
import org.openjdk.jmh.annotations.Threads;
import org.openjdk.jmh.annotations.Warmup;
import org.openjdk.jmh.infra.Blackhole;
import org.openjdk.jmh.runner.Runner;
import org.openjdk.jmh.runner.RunnerException;
import org.openjdk.jmh.runner.options.Options;
import org.openjdk.jmh.runner.options.OptionsBuilder;

//Test metric is throughput
@BenchmarkMode(Mode.Throughput)
//Warmup needed to exclude JIT compilation and JVM metric collection effects
@Warmup(iterations = 1)
//Thread count
@Threads(10)
@Fork(1)
//Test iterations
@Measurement(iterations = 50)
//Class instance lifecycle shared across all test threads
@State(value = Scope.Benchmark)
public class TestRandom {
	ThreadLocal<Random> random = ThreadLocal.withInitial(Random::new);
	ThreadLocal<SplittableRandom> splittableRandom = ThreadLocal.withInitial(SplittableRandom::new);
	ThreadLocal<SecureRandom> drbg = ThreadLocal.withInitial(() -> {
		try {
			return SecureRandom.getInstance("DRBG");
		}
		catch (NoSuchAlgorithmException e) {
			throw new IllegalArgumentException(e);
		}
	});

	@Benchmark
	public void testRandomInt(Blackhole blackhole) throws Exception {
		blackhole.consume(random.get().nextInt());
	}

	@Benchmark
	public void testRandomIntWithBound(Blackhole blackhole) throws Exception {
		//Avoid 2^n numbers as they're optimized but not typical application ranges
		blackhole.consume(random.get().nextInt(1, 100));
	}

	@Benchmark
	public void testSplittableRandomInt(Blackhole blackhole) throws Exception {
		blackhole.consume(splittableRandom.get().nextInt());
	}

	@Benchmark
	public void testSplittableRandomIntWithBound(Blackhole blackhole) throws Exception {
		//Avoid 2^n numbers as they're optimized but not typical application ranges
		blackhole.consume(splittableRandom.get().nextInt(1, 100));
	}

	@Benchmark
	public void testThreadLocalRandomInt(Blackhole blackhole) throws Exception {
		blackhole.consume(ThreadLocalRandom.current().nextInt());
	}

	@Benchmark
	public void testThreadLocalRandomIntWithBound(Blackhole blackhole) throws Exception {
		//Avoid 2^n numbers as they're optimized but not typical application ranges
		blackhole.consume(ThreadLocalRandom.current().nextInt(1, 100));
	}

	@Benchmark
	public void testDRBGSecureRandomInt(Blackhole blackhole) {
		blackhole.consume(drbg.get().nextInt());
	}

	@Benchmark
	public void testDRBGSecureRandomIntWithBound(Blackhole blackhole) {
		//Avoid 2^n numbers as they're optimized but not typical application ranges
		blackhole.consume(drbg.get().nextInt(1, 100));
	}

	public static void main(String[] args) throws RunnerException {
		Options opt = new OptionsBuilder().include(TestRandom.class.getSimpleName()).build();
		new Runner(opt).run();
	}
}

Changes in Java 17
#

Limitations of Previous APIs
#

  1. No unified interface: Previous Random and SplittableRandom lacked common inheritance or abstract interfaces. While their methods are largely identical and replacement isn’t too troublesome, this makes implementing custom random algorithms difficult due to the lack of unified interfaces.
  2. ThreadLocalRandom doesn’t play well with future Project Loom virtual threads. Virtual threads are continuously creatable resources, and using ThreadLocalRandom in a one-to-one mapping with numerous virtual threads would weaken randomness. We need new implementation methods and should start paving the way for Project Loom.

New API Definitions
#

Java 17’s JEP 356: Enhanced Pseudo-Random Number Generators unified random number generator interfaces under RandomGenerator:

image

For jumpability (simple calculations to skip many elements in sequence loops), there’s the JumpableGenerator interface, and for larger jump steps, LeapableGenerator.

For splittability (simple calculations to split generators producing completely different sequences), there’s the SplitableGenerator interface.

The correspondence between algorithms and implementation classes:

image

After unification, we can create different random number generators like this:

RandomGenerator random = RandomGeneratorFactory.of("Random").create();
RandomGenerator secureRandom = RandomGeneratorFactory.of("SecureRandom").create();
RandomGenerator splittableRandom = RandomGeneratorFactory.of("SplittableRandom").create();
RandomGenerator xoroshiro128PlusPlus = RandomGeneratorFactory.of("Xoroshiro128PlusPlus").create();
RandomGenerator xoshiro256PlusPlus = RandomGeneratorFactory.of("Xoshiro256PlusPlus").create();
RandomGenerator l64X256MixRandom = RandomGeneratorFactory.of("L64X256MixRandom").create();
RandomGenerator l64X128StarStarRandom = RandomGeneratorFactory.of("L64X128StarStarRandom").create();
RandomGenerator l64X128MixRandom = RandomGeneratorFactory.of("L64X128MixRandom").create();
RandomGenerator l64X1024MixRandom = RandomGeneratorFactory.of("L64X1024MixRandom").create();
RandomGenerator l32X64MixRandom = RandomGeneratorFactory.of("L32X64MixRandom").create();
RandomGenerator l128X256MixRandom = RandomGeneratorFactory.of("L128X256MixRandom").create();
RandomGenerator l128X128MixRandom = RandomGeneratorFactory.of("L128X128MixRandom").create();
RandomGenerator l128X1024MixRandom = RandomGeneratorFactory.of("L128X1024MixRandom").create();

Properties of Each Algorithm’s Random Number Generator Classes
#

1.Random: Based on Linear Congruential algorithm generating 48-bit numbers, with parameters ensuring every number can be generated, so Period = 2^48. nextInt and nextLong cannot achieve perfectly uniform random distribution because generated numbers are 48-bit, nextInt takes 32 bits, and nextLong combines two calls. As analyzed earlier, this algorithm cannot jump or split.

2.SplittableRandom: Based on SplitMix algorithm generating 64-bit numbers, MurMurHash ensures every number in range appears (Period = 2^64) with perfect uniform distribution. For nextInt, every result appears twice per period; for nextLong, every result appears once per period. As analyzed, this algorithm cannot jump but can split.

3.Xoroshiro128PlusPlus: Based on Xoroshiro128++ algorithm using two 64-bit numbers for state, these two numbers are never simultaneously zero, combining into one 64-bit random number. With two 64-bit numbers, there are 2^64 * 2^64 = 2^128 combinations, minus one (both zero), so Period = 2^128 - 1. This algorithm can jump but cannot split.

4.Xoshiro256PlusPlus: Based on Xoshiro256++ algorithm using four 64-bit numbers for state, these four numbers are never simultaneously zero, combining into one 64-bit random number. With four 64-bit numbers, there are 2^256 combinations, minus one, so Period = 2^256 - 1. This algorithm can jump but cannot split.

5. L64X256MixRandom: Based on LXM algorithm using one 64-bit number for Linear Congruential results and four 64-bit numbers for Xoshiro combination. Linear Congruential has 2^64 combinations, Xoshiro has 2^256 - 1 combinations, totaling 2^64(2^256 - 1) combinations, so Period = 2^64(2^256 - 1). This algorithm can split but cannot jump.

Other LXM implementations are similar.

image

You can see these properties in each algorithm implementation class’s annotations:

@Retention(RetentionPolicy.RUNTIME)
@Target(ElementType.TYPE)
public @interface RandomGeneratorProperties {
    /**
     * Algorithm name
     */
    String name();

    /**
     * Algorithm category
     */
    String group() default "Legacy";

    /**
     * Period size described by i, j, k:
     * period = (2^i - j) * 2^k
     */
    int i() default 0;
    int j() default 0;
    int k() default 0;

    /**
     * Equidistribution, 0 or max means non-uniform distribution
     * This value describes how many times each number appears in one period
     * Not perfectly precise, ignores small deviations
     * e.g., Xoroshiro128++ considers each number appears 2^64 times, not 2^64 - 1
     */
    int equidistribution() default Integer.MAX_VALUE;

    /**
     * Whether based on system Entropy (see SEED sources section)
     */
    boolean isStochastic() default false;

    /**
     * Whether hardware-assisted algorithm
     */
    boolean isHardware() default false;
}

We can also view each implementation’s properties and filter algorithms for our business needs through these APIs:

RandomGeneratorFactory.all()
	.map(fac -> fac.group()+":"+fac.name()
			+ " {"
			+ (fac.isSplittable()?" splitable":"")
			+ (fac.isStreamable()?" streamable":"")
			+ (fac.isJumpable()?" jumpable":"")
			+ (fac.isLeapable()?" leapable":"")
			+ (fac.isHardware()?" hardware":"")
			+ (fac.isStatistical()?" statistical":"")
			+ (fac.isStochastic()?" stochastic":"")
			+ " stateBits: "+fac.stateBits()
			+ " }"
	)
	.sorted().forEach(System.out::println);

Output:

LXM:L128X1024MixRandom { splitable streamable statistical stateBits: 1152 }
LXM:L128X128MixRandom { splitable streamable statistical stateBits: 256 }
LXM:L128X256MixRandom { splitable streamable statistical stateBits:384 }
LXM:L32X64MixRandom { splitable streamable statistical stateBits: 96 }
LXM:L64X1024MixRandom { splitable streamable statistical stateBits: 1088 }
LXM:L64X128MixRandom { splitable streamable statistical stateBits: 192 }
LXM:L64X128StarStarRandom { splitable streamable statistical stateBits: 192 }
LXM:L64X256MixRandom { splitable streamable statistical stateBits: 320 }
Legacy:Random { statistical stateBits: 48 }
Legacy:SecureRandom { stochastic stateBits: 2147483647 }
Legacy:SplittableRandom { splitable streamable statistical stateBits: 64 }
Xoroshiro:Xoroshiro128PlusPlus { streamable jumpable leapable statistical stateBits: 128 }
Xoshiro:Xoshiro256PlusPlus { streamable jumpable leapable statistical stateBits: 256 }

Which Algorithm is Fastest (Pretty Obvious Without Testing)
#

Based on our previous analysis, SplittableRandom should still be fastest in single-threaded environments, with ThreadLocalRandom fastest in multithreaded scenarios. The new random algorithm implementations require more computation as periods increase, and LXM implementations need additional calculations. These algorithms were added to accommodate more random applications, not for speed. However, to satisfy curiosity, here’s test code demonstrating the new RandomGenerator API’s convenience:

package prng;

import java.util.random.RandomGenerator;
import java.util.random.RandomGeneratorFactory;

import org.openjdk.jmh.annotations.Benchmark;
import org.openjdk.jmh.annotations.BenchmarkMode;
import org.openjdk.jmh.annotations.Fork;
import org.openjdk.jmh.annotations.Measurement;
import org.openjdk.jmh.annotations.Mode;
import org.openjdk.jmh.annotations.Param;
import org.openjdk.jmh.annotations.Scope;
import org.openjdk.jmh.annotations.Setup;
import org.openjdk.jmh.annotations.State;
import org.openjdk.jmh.annotations.Threads;
import org.openjdk.jmh.annotations.Warmup;
import org.openjdk.jmh.infra.Blackhole;
import org.openjdk.jmh.runner.Runner;
import org.openjdk.jmh.runner.RunnerException;
import org.openjdk.jmh.runner.options.Options;
import org.openjdk.jmh.runner.options.OptionsBuilder;

//Test metric is throughput
@BenchmarkMode(Mode.Throughput)
//Warmup needed to exclude JIT compilation and JVM metric collection effects
@Warmup(iterations = 1)
//Thread count
@Threads(10)
@Fork(1)
//Test iterations
@Measurement(iterations = 50)
//Class instance lifecycle shared across all test threads
@State(value = Scope.Benchmark)
public class TestRandomGenerator {
	@Param({
			"Random", "SecureRandom", "SplittableRandom", "Xoroshiro128PlusPlus", "Xoshiro256PlusPlus", "L64X256MixRandom",
			"L64X128StarStarRandom", "L64X128MixRandom", "L64X1024MixRandom", "L32X64MixRandom", "L128X256MixRandom",
			"L128X128MixRandom", "L128X1024MixRandom"
	})
	private String name;
	ThreadLocal<RandomGenerator> randomGenerator;
	@Setup
	public void setup() {
		final String finalName = this.name;
		randomGenerator = ThreadLocal.withInitial(() -> RandomGeneratorFactory.of(finalName).create());
	}

	@Benchmark
	public void testRandomInt(Blackhole blackhole) throws Exception {
		blackhole.consume(randomGenerator.get().nextInt());
	}

	@Benchmark
	public void testRandomIntWithBound(Blackhole blackhole) throws Exception {
		//Avoid 2^n numbers as they're optimized but not typical application ranges
		blackhole.consume(randomGenerator.get().nextInt(1, 100));
	}

	public static void main(String[] args) throws RunnerException {
		Options opt = new OptionsBuilder().include(TestRandomGenerator.class.getSimpleName()).build();
		new Runner(opt).run();
	}
}

Test results:

Benchmark                                                  (name)   Mode  Cnt          Score           Error  Units
TestRandomGenerator.testRandomInt                          Random  thrpt   50  276250026.985 ± 240164319.588  ops/s
TestRandomGenerator.testRandomInt                    SecureRandom  thrpt   50    2362066.269 ±   1277699.965  ops/s
TestRandomGenerator.testRandomInt                SplittableRandom  thrpt   50  365417656.247 ± 377568150.497  ops/s
TestRandomGenerator.testRandomInt            Xoroshiro128PlusPlus  thrpt   50  341640250.941 ± 287261684.079  ops/s
TestRandomGenerator.testRandomInt              Xoshiro256PlusPlus  thrpt   50  343279172.542 ± 247888916.092  ops/s
TestRandomGenerator.testRandomInt                L64X256MixRandom  thrpt   50  317749688.838 ± 245196331.079  ops/s
TestRandomGenerator.testRandomInt           L64X128StarStarRandom  thrpt   50  294727346.284 ± 283056025.396  ops/s
TestRandomGenerator.testRandomInt                L64X128MixRandom  thrpt   50  314790625.909 ± 257860657.824  ops/s
TestRandomGenerator.testRandomInt               L64X1024MixRandom  thrpt   50  315040504.948 ± 101354716.147  ops/s
TestRandomGenerator.testRandomInt                 L32X64MixRandom  thrpt   50  311507435.009 ± 315893651.601  ops/s
TestRandomGenerator.testRandomInt               L128X256MixRandom  thrpt   50  187922591.311 ± 137220695.866  ops/s
TestRandomGenerator.testRandomInt               L128X128MixRandom  thrpt   50  218433110.870 ± 164229361.010  ops/s
TestRandomGenerator.testRandomInt              L128X1024MixRandom  thrpt   50  220855813.894 ±  47531327.692  ops/s
TestRandomGenerator.testRandomIntWithBound                 Random  thrpt   50  248088572.243 ± 206899706.862  ops/s
TestRandomGenerator.testRandomIntWithBound           SecureRandom  thrpt   50    1926592.946 ±   2060477.065  ops/s
TestRandomGenerator.testRandomIntWithBound       SplittableRandom  thrpt   50  334863388.450 ±  92778213.010  ops/s
TestRandomGenerator.testRandomIntWithBound   Xoroshiro128PlusPlus  thrpt   50  252787781.866 ± 200544008.824  ops/s
TestRandomGenerator.testRandomIntWithBound     Xoshiro256PlusPlus  thrpt   50  247673155.126 ± 164068511.968  ops/s
TestRandomGenerator.testRandomIntWithBound       L64X256MixRandom  thrpt   50  273735605.410 ±  87195037.181  ops/s
TestRandomGenerator.testRandomIntWithBound  L64X128StarStarRandom  thrpt   50  291151383.164 ± 192343348.429  ops/s
TestRandomGenerator.testRandomIntWithBound       L64X128MixRandom  thrpt   50  217051928.549 ± 177462405.951  ops/s
TestRandomGenerator.testRandomIntWithBound      L64X1024MixRandom  thrpt   50  222495366.798 ± 180718625.063  ops/s
TestRandomGenerator.testRandomIntWithBound        L32X64MixRandom  thrpt   50  305716905.710 ±  51030948.739  ops/s
TestRandomGenerator.testRandomIntWithBound      L128X256MixRandom  thrpt   50  174719656.589 ± 148285151.049  ops/s
TestRandomGenerator.testRandomIntWithBound      L128X128MixRandom  thrpt   50  176431895.622 ± 143002504.266  ops/s
TestRandomGenerator.testRandomIntWithBound     L128X1024MixRandom  thrpt   50  198282642.786 ±  24204852.619  ops/s

From previous results, we already knew SplittableRandom performs best in single-threaded scenarios, while ThreadLocalRandom (similar algorithm but with multithreading optimizations) performs best in multithreaded environments.

How to Choose Random Algorithms
#

The principle: examine your business scenario to determine total possible random combinations and their range. Then find the algorithm with the best performance among those with periods larger than this range. For example, if your business scenario involves a deck of 52 cards (excluding jokers) with random dealing order:

  • First card: randomGenerator.nextInt(0, 52), choose from remaining 52 cards
  • Second card: randomGenerator.nextInt(0, 51), choose from remaining 51 cards
  • And so on

This gives us 52! total results, ranging between 2^225 ~ 2^226. If our random number generator’s period is smaller than this result set, certain card orders might never be generated. Therefore, we need a random number generator with Period > 52!.

Future Outlook
#

Random Number Generators in Project Loom
#

If Project Loom doesn’t optimize ThreadLocal, ThreadLocalRandom’s randomness performance will also degrade because virtual threads are object-like entities that can be continuously created and recycled. ThreadLocalRandom can’t enumerate infinitely. We might need to use fixed multiple random number generators for all virtual threads instead of ThreadLocalRandom:

ExecutorService vte = Executors.newVirtualThreadExecutor();
SplittableGenerator source = RandomGeneratorFactory.<SplittableGenerator>of("L128X1024MixRandom").create();
//Split into 128 different random number generators
List<RandomGenerator> rngs = source.splits(128);

AtomicInteger i = new AtomicInteger(0);

vte.submit(() -> {
    long random = rngs.get(Math.abs(i.incrementAndGet() & 127)).nextLong();
    ...
});

Random Number Generators with Scoped Local Features
#

Scoped Local is a more general domain variable (like ThreadLocal for current thread domain, Scoped Local can support different domains including virtual threads, threads, method domains, package domains, etc.). No version has been announced yet, but based on current leaks, we could use this approach to better assign random number generators to each thread:

private final static ScopeLocal<SplittableGenerator> rng_scope =
                                        ScopeLocal.inheritableForType(SplittableGenerator.class);

public static void main(String[] args) throws InterruptedException {

    SplittableGenerator rng1 =
            RandomGeneratorFactory.<SplittableGenerator>of("L128X1024MixRandom").create();
    SplittableGenerator rng2 =
            RandomGeneratorFactory.<SplittableGenerator>of("L32X64MixRandom").create();

    try (ExecutorService vte = Executors.newVirtualThreadExecutor()) {
        for (int i = 0; i < 5; i++) {
            ScopeLocal.where(rng_scope, rng1.split(), () -> { vte.submit(new Task()); });
        }
        for (int i = 0; i < 5; i++) {
            ScopeLocal.where(rng_scope, rng2.split(), () -> { vte.submit(new Task()); });
        }
    }
}

private static class Task implements Runnable {
    @Override public void run() {
        SplittableGenerator rng = rng_scope.get();
        System.out.println(rng);
    }
}

This comprehensive guide covers the evolution of random number generation in Java, from basic concepts to advanced implementations, providing practical insights for choosing the right algorithm for your specific use case. Whether you’re building simple applications or complex systems requiring high-quality randomness, understanding these fundamentals will help you make informed decisions about random number generation in your projects.

Related

OpenJDK JVM Deep Dive: Java Memory Model - A Comprehensive Guide to Concurrency and Memory Barriers
·12058 words·57 mins
A deep dive into Java Memory Model (JMM) from specification to implementation, covering memory barriers, CPU reordering, and Java 9+ VarHandle APIs. Learn about coherence, causality, consensus, and how volatile, final, and other synchronization mechanisms work under the hood with practical jcstress examples.
The Hidden Performance Killer: Why Code Location in Logs Can Destroy Your Microservice Performance
·898 words·5 mins
Discover how enabling code location in logs can cause severe CPU performance issues in microservices, especially reactive applications. This deep-dive analysis reveals the hidden costs of stack walking in Log4j2 and provides actionable solutions for high-throughput systems.
Tackling Performance Degradation in Sharded MySQL Tables: Understanding the Root Cause and Solutions
·1712 words·9 mins
A comprehensive guide to understanding why MySQL queries slow down over time in sharded environments, exploring the underlying causes of storage fragmentation and MVCC-related issues, and providing practical solutions using table rebuilding techniques with OPTIMIZE TABLE for maintaining optimal database performance.